
Yesterday the LIGO scientific collaboration announced that they had detected the gravitational waves from the in-spiral and merger of two black holes, shown in figure 1. It would not be an overstatement to say that this result has changed science forever. As a gravitational physicist, it is hard for me to put into words how scientifically important and emotionally powerful this moment is for me and for everyone in my field. But I’m going to try. This is my attempt to capture some of the science—and the poetry—of LIGO’s gravitational wave announcement.
The Source
About 1.3 billion years ago and as many light years away, two spinning black holes, each about thirty times the mass of the sun (one a bit bigger, one a bit smaller) ended their lives as separate entities. These two monsters had probably lived out many separate lives together: first as a binary system of two massive stars and most recently as two black holes orbiting each other. Somewhere in between, each one probably briefly outshone the entire galaxy as a core-collapse supernova.
But nothing lasts forever. Einstein tells us that mass distorts spacetime, warping distance and duration. And an accelerating mass (like a black hole in an orbit) releases some of its energy in ripples of this distortion. And so, over the billions of years of their shared lives, our black holes lost energy to these gravitational waves and their orbit decayed. They slowly, inevitably, spiralled towards each other.
As the partners approached, their orbit sped up and their slow, stately waltz gradually transitioned into a frantic tarantella toward coalescence. Eventually the partners came within about 10 kilometres of each other (people RUN that distance!). By this time, they were orbiting each other about thirty-five times per second!
The black holes spiralled towards each other at roughly the same rate about five more times before they suddenly plunged together, spinning around their shared centre of mass 250 times per second. But this stage didn’t last that long. Before even one second had passed, the black holes’ event horizons overlapped, and they merged into a single rapidly rotating object. This new single black hole oscillated wildly as it settled down into its final configuration, emitting gravitational waves all the while.
In-spiral. Merger. Ringdown. After (possibly) millions of years in a slowly decaying orbit, the final plunge took less than a fifth of a second. In those last moments, gravitational waves carried away ![]() Joules. That’s three times the energy contained in our Sun. Three suns, released as ripples in spacetime.
Joules. That’s three times the energy contained in our Sun. Three suns, released as ripples in spacetime.
This is a computer simulation of the in-spiral and merger of two black holes much like the ones I described, produced by my friends and collaborators in the Simulating Extreme Spacetimes (SXS) collaboration:
The SXS collaboration has written up their own explanation of the gravitational wave detection, including a ton of really awesome simulations and videos of the black-holes in question. Check it out here.
(Note, I previously had a rough back-of-the-envelope calculation of distances. However, the paper has the relevant information, which I am now using.)
Gravitational Waves
But what of the gravitational waves emitted by our ill-fated dance partners? These ripples in distance, in the very fabric of space and time, travel outwards from their source at the speed of light. Space is large and empty and it is mostly a lonely journey. Perhaps they pass through a cloud of gas and dust. Perhaps they don’t. If they do, the distortions of distance move the gas. Some gas particles move apart, some together. The gravitational waves might move a ring of gas particles, as shown in figure 2.

The effect is small; if the gas cloud were a few kilometres in width, the gas particles would move a distance less than one one-thousandth of the width of a proton. But they would move. And if they moved enough (they don’t) they would make a sound—the sound of the merging black holes:
Detection
Eventually, after about 1.3 billion years, on September 14th, 2015, the gravitational waves reached Earth. They were too weak to make a sound, but we could detect them. A gravitational wave is a distortion in distance, one that travels. So we can measure this distortion with a very precise ruler. And light is one of the best possible rulers.
Actually, we used two gigantic, perpendicular light-rulers, each several kilometres long. As a gravitational wave passed the rulers, it shrank distance in one direction and grew it in the other. The scientists who use these light-rulers call this discrepancy a “strain.” The paired light-rulers themselves are called “interferometers.”
We’ve built several interferometers to detect gravitational waves. There’s one in Livingston, Louisiana, which is shown in figure 3, and one in Hanford, Washington. There’s another in Sarstedt, Germany and another in Cascina, Italy. One, destined for India, is in storage. And another is under construction underground in Kamioka, Japan.

On that fateful day, only the detectors in Livingston and Hanford were active. (Some of the others aren’t even sensitive enough for their intended purpose. When people first started building gravity-wave detectors, it wasn’t clear how far away the sources would be.) The waves hit Livingston first, at exactly 3:50:45 AM local time. About seven-thousandths of a second later, they reached Hanford and distorted the light-ruler there, too. And a fifth of a second after that, they were gone. The sound of the black holes had passed us by and continued its journey into the void.

But they did not pass without a trace. No, the Livingston and Hanford detectors recorded their passage, shown beautifully in figure 4. The 1.3 billion-year-old waveform passed through our world and changed us forever.
Learning from the Waves
We already knew gravitational waves exist. That measurement took 30 years and won the Nobel prize. And we had a pretty good idea of what they should look like. But the only way to confirm that they looked like we expected was to observe them. So the first thing the LIGO team did was to use sophisticated statistical techniques, without any assumption about the final waveform, to extract the true wave from the noisy signal shown in figure 4.
They then compared that waveform to the wave predicted by general relativity. The two agree spectacularly. Score one for Einstein! Of course, there are possible modifications of general relativity such that a black hole in-spiral wouldn’t look any different. So only time, and more gravitational waves, will tell if those modifications are wrong. But for now, this result is a triumph of relativity.
Independently, the LIGO team matched the raw data to a “template bank” of possible gravitational waves, each generated for a different configuration of the black holes—different masses, different rotation rates, different orientations, et cetera. Eventually, they found a match. (Actually they found several, all of which were very similar.) And, fantastically, this match agreed perfectly with the wave extracted using the statistical technique. The extracted waveforms from the two detectors, calculated in both ways, are shown in figure 5.

As a huge bonus, matching the waveform in this way told the LIGO team the masses and rotation rates of the initial black holes and the final black hole that they became.
From the ripples in spacetime, we had extracted astrophysics!
Two Detections
I want to emphasize that one reason we can be so confident in the LIGO detection is that it happened twice, once for each detector. Both detectors are extremely sensitive—they could easily see an earthquake or a car driving down the highway and misinterpret it as a gravitational wave. But the gravitational wave was seen at both detectors, and the odds of them both getting exactly the same false positive are extremely low.
What We’ve Learned
In this one detection, we’ve learned a tremendous amount…some of it very definitive, some of it not. But at the very least, we now know the following:
- Gravitational waves look very much like we expected.
- Black holes definitively exist. No other two objects in the universe could have been so close before colliding. Of course, we had pretty good evidence that black holes existed before now.
- Binary black hole systems definitely exist. A few years ago, it was not obvious that these systems formed. To get a pair of black holes orbiting each other, you need a pair of supernovae. And that could easily destroy the orbit.
What We Stand to Learn
For most of the history of astronomy, humans relied on their unaided eyes to look at the stars. In the early 1600s, telescopes were invented and the universe opened up. Suddenly the twinkle of stars and planets resolved into gas giants and moons, clusters and nebulae and galaxies. In the 1930s, we discovered a new kind of telescope: the radio telescope. Once again, we saw space in literally a whole new light. Suddenly objects we thought we understood looked very different. And wild new things appeared, like radio pulsars. Every advance in telescope technology sparked a huge leap in our understanding of the universe. We could, essentially, see a whole new side of the universe.
This is just as big. Now we can hear the universe. We’re going to learn so, so much.
Related Reading
If you enjoyed this post and want to learn more about general relativity and gravitational waves, you may be interested in my series on how GR works:
- In Galileo Almost Discovered General Relativity, I explain the motivating idea behind general relativity and how Galileo almost figured it out.
- In General Relativity Is the Dynamics of Distance, I explain how simple arguments can tell us that gravity stretches or shrinks space and time.
- In General Relativity Is the Curvature of Spacetime, I describe how the distortion of distance and duration from gravity translates into curvature, and how this bends the path of light (and other stuff).
- In Distance Ripples, I explain how gravitational waves work.
- In Our Local Spacetime, I present a visualization of the curvature of spacetime near Earth.
- In Classical Tests of General Relativity, I explain a little history.
- In the Geodetic Effect, I talk about how we can use gyroscopes to directly measure the curvature of spacetime.
- The SXS collaboration has written up their own explanation of the gravitational wave detection, including a ton of really awesome simulations and videos of the black-holes in question. Check it out here.
Further Reading
Here are some nice lay resources on the recent LIGO discovery. (Thanks to Jonathan Chung on Google+ for finding some of these.)
- This is LIGO’s online press release. It contains, for example, a number of fantastic videos.
- In this video, Brian Green explains the take-home message.
- This is a great explanation of gravitational waves by quantum gravity physicist Sabine Hossenfelder.
- This is the lay article about the discovery by the American Physical Society.
- Googler Yonotan Zunger wrote up this nice explanation.
- This is a nice article by Brian Koberlein on the existence of black holes.
- This is the press release for the Nobel prize awarded for the indirect discovery of gravitational waves.
- This Nature article talks about several questions we can answer with gravitational waves.
- The New Yorker has a wonderful background piece on LIGO and gravitational waves.
Scholarly Reading
For the very brave, here are my academic sources.
- This is the LIGO detection paper. Already peer reviewed. Kudos to the LIGO collaboration for going through peer-review before announcing their result!
- This is the LIGO paper describing how they extracted the mass and spin of the black holes.
- This paper describes the LIGO team’s investigation of whether or not the December detection could have been a mistake. (Obviously, they concluded it was real, or I wouldn’t be writing this blog post…)
- This paper describes the LIGO team’s model-agnostic approach to measuring the wave. This is how they know they’re not falling victim to wishful thinking.
- This technical paper describes how the LIGO team estimated their noise and error.
- This paper discusses how we’ve tested general relativity with this observation.
- This is an assessment of the rates of black hole binary mergers in the universe based on the measurements LIGO has made so far.
- This is a related paper on what that means for detectors.
- This paper is a search for neutrinos from the black hole merger that LIGO observed. (None were found.)
- This is the population model for binary black holes which may be wrong.

Jonah, thanks and thanks again for this fabulous article. It’s a technical tour de force, but also sheer poetry! Your love for the science, and your exhilaration at this breakthrough moment, shine through.
Reading it, I experienced one “aha!” moment that I’d like to ask about: I realize light that’s inside the event horizon of a black hole can’t escape, because that’s the point where the “escape velocity” becomes higher than the speed of light itself. I also assumed this applied to any form of energy, so that literally nothing could escape.
But if I read you aright, energy can and does escape from a black hole via the gravitational wave. Does this mean gravitational waves are not bound by the same escape velocity as other waves? Is this because it’s gravity itself that defines the escape velocity? And finally, might a black hole keep emitting gravitational waves long enough to burn itself out and cease to be a black hole?
Wow, thank you, Gary! That’s really high praise! 🙂
That’s a great question too! No, nothing can escape the event horizon, not even gravitational waves, which travel the speed of light. But the energy of a black hole isn’t JUST contained within the event horizon. It is also contained in the gravitational field surrounding the black hole. Think about an electron. The electron carries mass, which is a form of energy, but it also carries other types of energy. It has kinetic energy, for example, from its motion. And when you move another electron towards it, you must do work. you are putting energy into the system, which is stored in the electric field between the electrons.
And if you accelerate an electron, some of its kinetic energy will be put into the electric field as a wave, which we call light.
It’s the same with black holes. Except now it’s a gravitational field.
One thing I’ve been wondering about — when two masses are orbiting, the energy contained in the gravitational waves they produce is extracted from their mutual orbit. But that three solar masses of energy emission was extracted from the black holes’ masses.
The question is — did this extraction happen purely as a “bookkeeping measure” because there was no mutual KE left to get the energy from (seems unlikely: the whole reason the final merger emitted gravitational waves at all was because acceleration was still happening), or was it happening all along? (i.e., do orbiting objects routinely lose nanoscopic amounts of mass in addition to their mutual KE loss due to gravitational waves?)
(Now I’m wondering what the heck is accelerating in the ringdown phase. The answer is probably “spacetime itself” or something like that: the event horizons are still distorted, but answering why would probably require terrifying maths.)
Great questions, Nick!
Regarding the “mass from the black holes” no it was not a “book-keeping” measure. It’s a combination of it happening all along, as you describe, and of the the fact that black holes don’t just HAVE gravity, they partly ARE gravity. Let me explain. Einstein’s famous field equations:
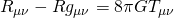
tell us that energy curves spacetime. But the curvature of spacetime itself carries energy. And so it curves spacetime even more. This curvature-feeding-on-itself is one way of expressing that gravity is nonlinear. This is, in fact, why things like event horizons can form. So, in effect, the gravitational field from each black hole carries and contributes to the mass of the black hole. Does that make sense?
Regarding the ringdown phase. Yeah, the answer is “spacetime itself.” 🙂 The technical term is “quasinormal modes” which are oscillations in the spacetime of and around the black hole.
https://en.wikipedia.org/wiki/Quasinormal_mode
And indeed there is scary math. Here it is:
http://relativity.livingreviews.org/Articles/lrr-2003-6/
Regarding whether or not a black hole can emit gravitational waves so much that it ceases to be a black hole… This was a question people investigated seriously for a long time. In the right circumstances, the answer is yes! But you need to keep making it wobble. Otherwise it’ll eventually stop wobbling and settle down. For example, if you can somehow take a gravitational wave and make it pass by a spinning black hole, it can actually suck up more of the black hole’s energy, making more gravitational waves. This is called the superradiant instability and it’s a form of Penrose process: https://en.wikipedia.org/wiki/Penrose_process
However, in a realistic astrophysics simulation, that won’t happen… at least, to my knowledge.
As Einstien said, if you cant explain something simply, you dont understand it well enough. You obviously do understand it, because I now do, up to a point. The beauty of the event itself is breathtaking to a simple layman like myself, I can understand your excitement. When I look at the pictures I see a giant vaccuum cleaner bag, or 2, having sucked in everthing around them, exploding and ejecting the minute particles which bond the universe together. Like an endless heartbeat. Many thanks for all your hard work.
Thanks for reading, Andrew! That’s high praise! I’m glad I was able to convey some of my enthusiasm! 🙂
Is this aether revisited, with the waves being gravitational, not electromagnetic?
Good question! Not really. Gravitational waves travel at the speed of light, just like light waves do… and the speed of light is still constant, no matter your reference frame.
They’re really a lot like electromagnetic waves… except that the thing wiggling is spacetime, not electric and magnetic fields.
Thank you for the great explanation. Is there a connection between GW’s and inflation? Could future detectors distinguish between theory’s?
Thanks for reading! 🙂
There is a connection! The prediction from inflation is that fluctuations in the infalton field (which causes inflation) should cause fluctuations in spacetime, which manifest as gravitational waves. LIGO is only sensitive to gravitational waves from astrophysical sources. And even the planned space-based detector LISA is only sensitive to supermassive black holes.
But eventually yes, we plan to build a detector that can detect primordial gravitational waves, the Big Bang Observer:
https://en.wikipedia.org/wiki/Big_Bang_Observer
It’s decades away though. Even LISA is decades away. And the BBO is basically LISA but bigger.
Fantastic article! Though I’m a bit upset that those black holes cause my body to be stretched one direction and squished in another. I mean, what’s up with that? What right does black holes have to disrupt everything? It’s bad enough they have to gobble up everything placed in front of them. Do they think they are Stephen King’s Langoliers? You know if you think about the mini series. Stephen King’s story comes interestly close, as portrayed in the movie, time stops and Langoliers gobble everything up, just like a black hole.
I was thinking on my midnight walk of what if a black hole entered our solar system. We’re doomed to be consumed by the blackened monster. No way to escape its grasp. All the earth’s achievements soon to be disassembled. Ok, enough about that nightmare. 🙂
I’m super excited that we now have a new tool (one in my backyard) to explore the universe. It’s like the invention of the first telescope. A tool that will constantly improved and expanded on to further our understanding of the universe. We live in a great time!
Thanks for reading, Captain Jack!
Indeed, and what right does a passing car have to push at your body with pressure waves. It’s very rude! 🙂 As you can probably tell, I too am very excited about gravitational waves and I’m happy to share my enthusiasm! 🙂
Jonah,
Yeah, every time I’m walking on the sidewalk and a 18 wheeler or bus I cringe because I know the pressure wave is going to pick up some dirt and fling it into my eyes, or on rainy days, blow out my umbrella.
So.. I have a question. Maybe I’m just reading this wrong. I’m confused how 1.8x(10^47) J is equal to three times the energy in our sun? https://en.wikipedia.org/wiki/Orders_of_magnitude_(energy)
“theoretical total mass-energy of the Sun”
I think you caught a typo/mistake in my post. I should have written 5.4×10^(47) Joules, not 1.8×10^(47). Thanks for the catch!
The links on this page don’t work, perhaps you can fix them? thanks. My question is about the dark port at LIGO, the place where light comes out if the phase shifts. It’s also called the antisymmetric port, does that mean it only detects a difference in phase, or is there a way to tell whether the distance to the mirror gets longer or shorter?
Thanks for reading, David. Can you specify which links aren’t working for you? They all seem to work for me.
LIGO only detects a phase difference, which corresponds to one arm growing with respect to the other. If both arms grow or shrink the same amount, LIGO won’t see anything.
Hi, thanks. The links work, it’s just that the underlines were faint. The question was about whether when one arm grows in length, and the other contracts, does the light from the port tell us which does which?
Ah I see. No the port won’t tell us which does which, at least I don’t think it will. Somebody who works on the actual instrument might know of a clever trick.
Hi Jonah,
first, let me join the chorus praising your article 🙂
About the question which arm contracts and which one lengthens: I hear from the detector people that nowadays the dark port is not kept completely dark, but at a very small intensity. This allows distinguishing which arm contracts: If the intensity in the dark port diminishes, it’s one arm, if it increases slightly, it is the other.
Hi Professor Nollert,
I’m glad you liked it! 🙂
I wasn’t aware of that—that’s quite cool! Thanks for this interesting tidbit.
Thanks. I’m trying to understand how the wave relates to curvature. Is there an equivalent to the compression made by the wave within the way we describe curvature? I know the strain is the difference in distance between objects over the normal distance between them, and that the pattern alternates in two directions at right angles, (the position of which is presumably set by the wave’s direction of motion).
But anything that can be linked to that, coming from curvature, would help – I’ve read that the strain is ‘the deviation in the spacetime metric from its nominal form’. Can you tell me how one would derive, in an ordinary static spherical gravity field, ‘the deviation in the spacetime metric from its nominal form’ at a given point in the field? Perhaps they can be linked in that way.
I’ve actually written a whole series on that! I list the first few below. You ask in particular about how one would derive gravitational wave strain from a spherical gravitational field. This is not actually possible because in a perfectly spherically symmetric system, there are no gravitational waves. There has to be some slight asymmetry. One can, however, derive the distortion of distance. I actually visualize that in one of my articles I link to below. The distortion comes from Einstein’s equations which define the distortion (and the change of the distortion) in terms of the matter content of the universe.
http://www.thephysicsmill.com/2015/07/26/galileo-almost-discovered-general-relativity/
http://www.thephysicsmill.com/2015/08/03/general-relativity-is-the-dynamics-of-distance/
http://www.thephysicsmill.com/2015/08/15/general-relativity-is-the-curvature-of-spacetime/
http://www.thephysicsmill.com/2015/08/23/distance-ripples-how-gravitational-waves-work/
http://www.thephysicsmill.com/2015/09/06/our-local-spacetime/
Thanks, I’ve looked through these, couldn’t find an answer to my question. I know that there are no gravitational waves in a spherically symmetric field, that’s why I mentioned it. I’m looking for analogies between that state and what happens within the wave. For instance, if the wave is like a moving curved dimple in space, just as the static field is like a non-moving curved dimple, then the difference in distance expressed by h, the strain term, might be similar to some other term, such as the differences in distance we find in the radial direction in a static field. Or perhaps not in the radial direction, in some ways of looking at GR, distances change across the field in other ways. I know that the actual GR distances don’t change (and I know you don’t take the extra dimension too literally, as some do), but the 3D distances do change. So is a gravitational wave the same? is the difference in distance a difference in 3D distance, while the GR distance (4D for some), stays the same?
If you want to try and imagine what a gravitational wave looks like, think of space “popping out” in one direction and “scrunching up” in another. That’s what the strain means.
Distances in general relativity definitely do change. You are probably thinking of the spacetime interval, which is invariant under coordinate transformation and thus doesn’t change when you change speed. But the interval does change when you travel through the spacetime. This is actually one definition of what it means for spacetime to be curved. A gravitational wave is a distortion in distance (and duration) that travels. And it is a real, physical distortion. The spacetime interval near the gravitational wave changes.
Nothing to do with travelling through spacetime. I meant that curvature with a static mass has distances (some say rulers), changing length. But those are Euclidian distances. The GR distances, as John Baez says, don’t change due to curvature. I wondered if the alteration to distances when the wave distorts them is similar, as I have the mathematics for one, but not for the other.
The very definition of cuvature is that distances change, both Euclidean and Minkowskian. Can you point me to where John says that? He know his stuff, so I think there must be a mis-communication or mis-interpretation going on here.
Well, one must be careful—absolute distances are not possible to measure. But it’s certainly meaningful to say that distances change with respect to each other.
I don’t know if I can find it, might be as you say, a miscommunication. Thanks for your help.
Perhaps you can help in this way – the time rate goes up and down with the peaks and troughs of the waves. I found this quote from Kip Thorne:
‘The colliding black holes that produced these gravitational waves created a violent storm in the fabric of space and time, a storm in which time speeded up, and slowed down, and speeded up again, a storm in which the shape of space was bent in this way and that way’.
Can you tell me how the time rate (at a peak or a trough) is related to the strain term h, which is (difference in distance) / (normal distance)? Thanks.
It’s difficult to extract the rate of flow of time from the distortion in distance because, depending on how fast you’re moving and where you are, one can completely become the other. In one reference frame, the distortion is all in the difference in distance between LIGO’s mirrors. In another, it’s all in the rate of the flow of time.
But, roughly, the strain tells you how much quicker time flows in one arm of the LIGO interferometer than the other.
Does that help?
I meant in the earth’s frame. so I guess the time rate is altered by the same factor difference as distances are. Thanks, that helps.
You sound like those time rate changes are SR type ones. Or are they GR type time rate changes?
But this bit is like nothing from either SR or GR:
“In one reference frame, the distortion is all in the difference in distance between LIGO’s mirrors. In another, it’s all in the rate of the flow of time.”
But instead, we can say it can be taken in one way or another within an individual frame. But that’s SR, I’m thinking they’re really more like GR time rate changes, which is what Kip Thorne said suggested. Do you agree?
Ah sorry for the confusion. The fact that there is a distortion at all is general relativity. The fact that it can manifest as space or time or both is special relativity.
Thanks. I’m wondering if the distance that gets compressed, in that way of looking at it, is a Euclidian distance, or a GR distance (3D or 4D, if you like).
In a gravity field the Euclidian straight line distances are always shorter. (And the passing wave will have some aspects of a gravity field).
In the Shapiro time delay – if these things are taken literally, as some do – the light has to travel the longer, curved route, which creates part of the delay.
So a compression of the straight line distance might leave the laser having to travel the longer route. If so, the path length might stay the same, it just briefly gets curved as the wave passes by.
If that’s right, then time rate changes are effectively what cause the signal, because distance changes would not alter the light’s journey time at all. Does that fit with your view of it?
The quantity that changes is called the proper time, which is the spacetime interval. To translate into the language you’re using, I think that’s a “4D GR distance.”
You seem to be trying to fix the point of view and say it’s “only” a time delay or “only” a space delay. That is not the ideal way to look at thing: both for gravitational waves and for Shapiro time delay. Because of special relativity, it is not possible to disentangle the two.
I explain what the spacetime interval is (albeit only in special relativity) here:
http://www.thephysicsmill.com/2013/02/10/a-space-time-cocktail-minkowski-space-and-special-relativity/
In general relativity, the interval changes length depending on where you are in spacetime.
Thanks for that, I see what you mean. I didn’t mean space and time can be disentangled in any fundamental way, but we can still look at distances without thinking about the time it takes to travel them (for light or matter). When you do that, GR distances in a gravity field are still slightly longer than the Euclidian distances.
But it seems to me you’re saying that both space and time distances are altered by the factor 1 +/- h (h is the strain term). If so, do time intervals get shorter (time speeds up) when space distances get longer, and vice versa? That can’t be, you’d get a cancellation. LIGO would get no signal.
So perhaps time intervals get longer (time slows down) when space distances get longer. Then you’d get a double effect. Do they allow for a double effect, as we do with some other effects, which may be different, but which include the Shapiro time delay, and the deflection of light?
Both space and time are altered such that LIGO measures a strain of h. The strain LIGO measures will stay the same whether the distortion is all space or all time. Or, somewhere in the middle where it’s some space and some time.
The same is true for Shapiro time delay (which you can in fact think of as a stretching of space in the proper reference frame).
And when it’s equal between space and time, can we quantify the strain on each?
And can we stop space and time moving around by just taking the frame where the earth is still and so is LIGO, and ask all the people who work there to keep still for a minute?
Yes it’s possible to quantify the strain on each, though I don’t have that calculation off the top of my head.
If we could travel at the speed of light, along with the wave, it would be possible to stop things from changing, but otherwise it’s not possible… for the same reason you can’t transform a light wave into a static electric field: the speed of light is constant, no matter your reference frame. I wrote about that here:
http://www.thephysicsmill.com/2012/11/19/the-speed-of-light-is-constan/
So the strain on each would be nearer 1, and combining them you’d get 1 + h.
And it seems that for the space and time components not to cancel, the part of the wave that creates longer distances is where the time rate gets slower, rather than the other way round?
Yes exactly right. But it’s not obvious that that’s the case. When gravitational wave detectors were first proposed, people had to carefully work out the effect to make sure that it’s measurable.
Thanks a lot for your help Jonah
I’m glad I could help. 🙂